Das Programm GraspableMath habe ich schon vor einiger Zeit kennengelernt und auch erfolgreich im Mathe-Unterricht in Klasse 8 eingesetzt. Damals ging es darum, dass die Schüler lernen sollten wie sie eine Gleichung nach einer beliebigen Variablen auflösen können. Das geschah im Zusammenhang mit dem Auflösen von Gleichungen mit einer Variablen.
Allerdings habe ich mir schon einige Zeit darüber Gedanken gemacht, wie ich GraspableMath früher einsetzen kann. Denn GraspableMath beherrscht ja perfekt alle Rechenregeln und daher stellt sich die Frage, warum man es nicht schon im Rahmen der Einführung von Rechenregeln verwenden kann. Der Artikel ist im Grunde genommen Unterrichts-Material, dass man direkt einsetzen könnte. Da die Schüler erst einmal lernen müssen, wie man GraspableMath bedient, habe ich kurze Gifs erzeugt, die das zeigen.
Das Material ist nach Ideen des Dialogisches Matheunterrichts aufgebaut, die das „Ich-Du-Wir“ Prinzip nutzt.
Ich würde mich über Kritik und Meinungen, Einsatzberichte falls ihr es mal mit Schülern ausprobiert und Anregungen aller Art in den Kommentaren freuen.
Einstieg
Das Rechnen mit großen Zahlen sollte für dich hoffentlich kein Problem mehr darstellen. Und auch mehrere Rechnungen, die hintereinander ausgeführt werden müssen, solltest du schon ein wenig Erfahrung haben. Aber schau dir mal die folgenden Rechnungen an … das ist schon heftig, oder?
Da sind so viele Rechnungen mit Plus, Minus und auch Mal hintereinander, da weiß man gar nicht, so man anfangen soll? Oder fängt man einfach von vorne an? Oder gibt es eine Rechnung in der langen Rechnung, mit der man am besten anfängt, weil dann alles folgende einfacher wird?
Das zu erforschen, soll nun deine Aufgabe sein.
Als Forschungs-Hilfsmittel, soll dir das Programm GraspableMath dienen. Der Name kommt vom englischen Verb „to grasp“ = greifen. Dabei geht es unter anderem darum Mathematik begrifen zu können indem man es angreift. Was mit dem angreifen gemeint ist, wird im folgenden Abschnitt anhand von kurzen Filmsequenzen erklärt.
Bedienung von GraspableMath
Hier ein paar grundlegende Informationen zur Nutzung zur GraspableMath. Schau dir die Filmsequenzen an und lies den Text dazu. Versuche es dir zu merken. Wenn du nachher GraspableMath sollst, kannst du notfalls hier noch einmal nachschauen.
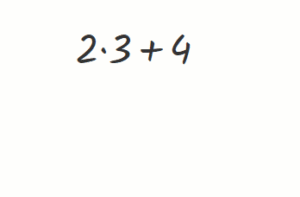1.) Rechnungen durchführen und gesamten Rechenweg zeigen
Links im Bild siehst du eine Rechen-Aufgabe. Du kannst einen Teil der Rechnung ausführen, hier die Multiplikation von 2 mal 3, indem du das Rechenzeichen anklickst. Statt der ursprünglichen Rechnung erscheint dann erst einmal die vereinfachte Rechenausdruck. Willst du die ursprünglichen Aufgabe anzeigen, ziehst du den Doppelknopf hinter der Rechnung herunter und „klappst“ so alle Rechenschritte aus. Du könntest auch umgekehrt die Rechenschritte einklappen.
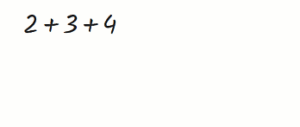2.) Rechnungen kopieren
Damit du verschiedene Rechenwege ausprobieren kannst, solltest du dir eine Rechen-Aufgabe kopieren. Dazu ziehst du mit der linke Maustaste hinten am Knopf hinter der Aufgabe und lässt die linke Maustaste erst los, wenn der Mauszeiger weit genug weg von der kopierten Aufgabe ist. Falls sie sich überlappen, kannst du die Rechnungen auch verschieben.
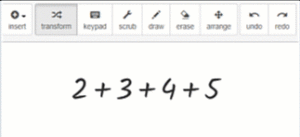3.) Rechnungen zurücknehmen (undo)
Wenn du eine Aktion rückgängig machen willst, dann brauchst du den Werkzeug-Knopf „undo“, der jede Aktion rückgängig macht. Du kannst immer wieder eine Aktion rückgängig machen und auch mehrere Aktionen hintereinander, wenn du vorher mehrere Aktionen durchgeführt hast.
4.) Aufgaben verschieben und löschen
Falls beim Kopieren zwei Aufgaben übereinander liegen, dann solltest du sie verschieben können. Dazu gibt es zwei Möglichkeiten:
Bewege den Mauszeiger links vorne an eine der Aufgaben bis sich der Mauszeiger verändert. Dies ist sozusagen eine geheime Stelle, an der du eine Aufgabe verschieben kannst. Wenn die zwei oder mehr Aufgaben ungünstig übereinander liegen kannst du auch das Werkzeug „arrange“ (zu deutsch: Anordnen) verwenden. Klicke den Werkzeug-Knopf an und nun kannst du die Aufgaben überall anfassen.
Gleichzeitig erscheint rechts oben an den Rechnungen ein Kreuz, mit dem du einen Aufgabe/Rechnung löschen kannst.
5.) GraspableMathe rechnet nur das was erlaubt ist
Was ist den bisherigen Filmsequenzen nicht zu sehen war: GraspableMath rechnet nur das, was man auch rechnen darf. Wenn du einige der Rechenzeichen anklickst, wird GraspableMath sozusagen den Kopf schütteln und dich darauf hinweisen, dass man das nicht rechnen darf, indem das Rechenzeichen mit den betreffenden Zahlen leicht wackeln. Das ist genau das, was dir helfen wird!
Deine Aufgabenstellungen
SCHRITT 1: Schau dir noch einmal die drei langen Aufgaben an. Dein Auftrag wird es sein, mit Hilfe von GraspableMath heraus zu bekommen, welche der vielen Rechnungen man zu Beginn durchführen kann.
Öffne dazu das GraspableMath Aufgabenblatt in einem Browser-Tab und schreibe die erste Aufgabe ins Heft. Verwende als Überschrift: Welche Rechnung darf zuerst durchgeführt werden?
Kopiere dir nun die erste Rechnung (siehe Anleitung 2.) und probiere aus, welche Rechenzeichen (also Plus, Minus und Mal) du anklicken kannst, so dass die Rechnung ausgeführt wird. Klicke dazu einfach alle Rechenzeichen an und schaue, ob etwas passiert.
Markiere parallel zu deinen Versuchen auf der abgeschrieben Aufgabe mit zwei verschiedenen Marker-Farben, das Rechnenzeichen, zu dem man die Rechnung durchführen kann.
- Verwende eine Farbe (z.B. gelb) für Plus- und Minus- Rechnungen.
- Verwende eine andere Farbe (z.B. blau) für Mal-Rechnungen
SCHRITT 2: Schau dir die markierte Aufgabe an. Betrachte jedes der Rechenzeichen und die Zahlen, die davor und danach stehen. Und schau dir auch an, welche Rechenzeichen davor und nach auch noch stehen. Kannst du erklären, woran man an der langen Rechnung erkennen kann, ob eine Rechnung durchgeführt werden kann oder nicht. Tipp: Es hängt von den anderen Rechenzeichen ab, die an die Zahlen angrenzen.
Versuche deine Ideen aufzuschreiben. Fange zum Beispiel so an:
- Man darf in der Aufgabe 2+3 nicht rechnen, denn …
- Man darf 3⋅4 …
Versuche, wenn möglich, zu jedem Rechenzeichen zu beschreiben, woran man erkennen kann, dass die Rechnung durchgeführt werden darf oder nicht. Wenn du nicht sicher bist, dann probiere erst einmal Schritt 3.
SCHRITT 3: Falls du schon verstanden hast, welche Rechnung man bei einer größeren Aufgabe durchführen kann, dann kannst du das bei der zweiten Aufgabe ausprobieren. Schreibe dir dazu wieder die Rechnung ins Heft auf und markiere wie vorher mit Farben, was du vermutest, welche der Rechnungen aller Rechenzeichnen man durchführen kann. Vergleiche dazu mit der ersten Aufgabe und versuche ähnliche „Rechenkonstruktionen“ zu finden. Wenn du fertig bist, kopiere die zweite Aufgabe auf dem GraspableMath Aufgabenblatt und teste deine Vorhersagen. Mache einen deutlichen roten Haken an eine Rechenzeichen, wenn du es richtig vorhergesagt hast und ein deutliches f, wenn es falsch war.
Falls du die Prinzipien bei der Aufgabe 1 noch nicht verstanden hast, probiere wie beim ersten Mal alle Rechenzeichen durch und markiere wieder wie vorher beschrieben.
SCHRITT 4: Kontrolliere deine Vermutungen aus Schritt 2. Hattest du recht? Falls du nicht alles richtig, dann versuche bei diesen eine neue Begründung zu finden und korrigiere notfalls deine Ausssagen bei Aufgabe 1.
SCHRITT 5: Probiere nun bei der dritten Aufgabe, um du verstanden hast, wann eine Rechung zu Beginn durchgeführt werden darf oder nicht. Markiere die Rechenzeichen wieder und teste deine Vermutungen. Hast du einen Fehler gemacht, versuche zu begründen, warum man eine Rechnung nicht durchführen kann.
SCHRITT 6: Schau dir noch einmal alle Aufgaben und die Rechnungen darin an. Versuche nun eine Zusammenfassung zu schreiben, in der du beschreibst, woran man bei einer beliebigen Rechnung in einer länderen Aufgabe erkennen kann, ob man die Rechnung durchführen kann oder nichts. Erstelle dazu eine eigene Aufgabe und beschreibe daran die von dir festgestellten Rechenregeln.
Probiere deine erfundene Aufgabe in GraspableMath aus und kontrolliere, ob du selber keinen Fehler gemacht hast. Um eine eigene Aufgabe zu erstellen, musst du die linke Maustaste länger drücken, bis ein bunter Kreis erscheint. Wähle den Abschnitt rechts oben mit f(x) aus, klicke den breiten Eingabebereich an und gib deine Aufgabe ein. Klicke „Done“ (deutsch: erledigt) an, um die Eingabe zu beenden.
Das GraspableMath-Arbeitsblatt
Benutze das GraspableMath Arbeitsblatt unter diesem Link.
Vergleich mit einem Mitschülern
Suche dir einen Mitschüler, der soweit wie du ist. Stellt euch eure Regeln vor und diskutiert deren Gültigkeit. Falls dein Mitschüler eine Formulierung hat, die dir besser gefällt, notiere dir in deinem Heft eine alternative Formulierung neben deinem ersten Versuch.
Stellt euch eure eigenen Aufgaben vor und begründet bei der Aufgabe des Mitschülers, woran man erkennen kann, das man eine Rechnung durchführen kann oder nicht.
Besprechung in der Klasse
Mit der Klasse werden wir die Ergebnisse einzelner Schüler vorstellen. Abschließend formulieren wir gemeinsam allgemeingütige Regeln, wie man bei längeren Aufgaben vorgehen kann.
Antworten