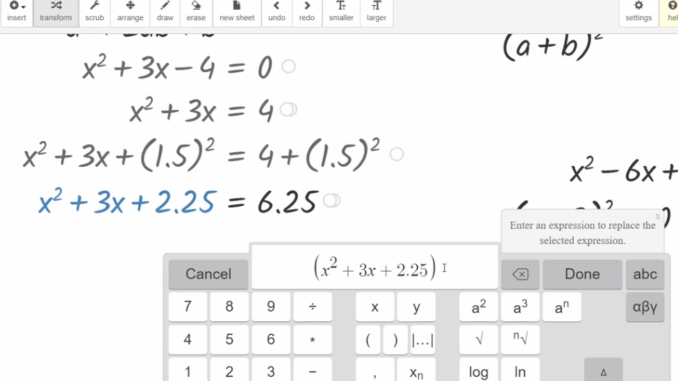
Über GraspableMath habe ich ja schon ein paar Mal geschrieben. Nach wie vor sehe ich großes Potential in dem Werkzeug. Hier eine Idee, wie man die Schüler selbstständig, vielleicht im Sinne von Flipped Classroom, die Quadratische Ergänzung erlernen können und dann vielleicht auch selbstständig die pq-Formel herleiten können. Dabei macht man sich zunutze, dass GraspableMath die Aktivitäten/Umformungen des Schülers überwacht und dafür sorgt, dass sich der Schüler auf die Idee der quadratischen Ergänzung konzentrieren kann.
Grundidee Flipped Classroom
Viele denken bei Flipped Classroom vor allem an die Arbeit mit Videos, in dem Sinne, dass in einem Video erkläre wird, wie man eine Aufgabe rechnet. Ich verstehe Flipped Classroom allgemein vor allem im Sinne von Auslagern von Aktivitäten, die keine Kommunikation bedürfen, auf die Hausaufgaben. Das kann auch einfach mal das Abschreiben von Regeln oder die Kontrolle von Übungen sein.
Bei dieser Idee hier mache ich mir, wie schon erwähnt, die Fähigkeit von GraspableMath zu Nutze, dass der Schüler in seinen Aktivitäten kontrolliert wird. Er bekommt bei der Anwendung der Idee der quadratischen Ergänzung von GraspableMath ein Rückmeldung, falls er eine falsche Idee umsetzen will bzw. er kann am Ergebnis sehen, dass seine Idee nicht das gewünschte Ergebnis liefert.
Da brauche ich nicht zuschauen, der Schüler kann erst einmal mein vorgegebenes Beispiel nachvollziehen, um die Bedienung von GraspableMath zu üben und sollte zum richtigen Ergebnis kommen. Bessere Schüler sollte es damit locker schaffen, die weiteren Beispiele zu bearbeiten.
Thema Quadratische Ergänzung
Die Quadratische Ergänzung ist ein typisches Beispiel, wo man in Mathematik den Schülern zeigen kann, wie man mit recht einfachen Mitteln zu einer allgemein anwendbaren Formel kommen kann, die bei vielen Aufgaben nutzbar ist.
Ziel ist es die Lösungen für eine quadratische Gleichung zu finden, indem man mit Hilfe einer Binomischen Formel ein Quadrat (also eine Produkt) erzeugt, von dem man über die Wurzel Lösungen finden kann.
Die Schüler kennen schon die Binomischen Formeln (und haben sie vermutlich wieder vergessen) und wissen grob, wie man eine Gleichung durch Äquivalenzumformungen auflösen kann. Bei quadratischen Gleichungen geht das so aber nicht.
Arbeitsaufträge für die Nutzung von GraspableMath
Die Arbeitsaufträge sind sicher für einmal Hausaufgaben zu viel. Aber man könnte zumindest die Aufgabe 1 daheim bearbeiten lassen. Teil b.) bereitet eventuell einige Schülern Probleme, daher wäre das die Stelle, wo zu Beginn der nächsten Stunde die Schüler in Gruppenarbeit ihre bisherigen Überlegungen vergleichen und ergänzen könnten.
Funktioniert es?
Leider habe ich seit einiger Zeit keine 9. Klasse gehabt und werde in nächster Zeit eher auch keine haben. Daher kann ich es also nicht testen. Allerdings habe ich einen 8-Klässler als Testperson in meinem Haushalt 😉 und der durfte eben das Video mit der Anleitung anschauen und hat dann das Beispiel nachvollziehen können.
Abgesehen, dass er beim Umschreiben der Formel zu hektisch gewackelt hat und darauf das Programm nicht reagiert hat, war die Auswahl eines Teiles der Formel so wie gezeigt nicht wirklich möglich. Allerdings kann man auch die gesamte Gleichung schütteln (z.B. am Gleichheitszeichen festhalten) und dann die linke Seite umschreiben. Ich sollte also vielleicht das Video noch einmal ändern. Er kennt auch noch nicht das Konzept der Wurzel-Berechnung, aber wenn man weiß, dass man die „hoch 2“ einfach rüberziehen muss und doppelt auf das Wurzel-Symbol klicken muss, muss man die Wurzel an sich nicht kennen.
Bei den Beispiel-Aufgaben (die ich noch ändern muss) hatte er eigentlich kein Problem. Er hatte das Video an der Stelle angehalten, wo die Beispiel-Rechnung insgesamt zu sehen war und konnte daran erkennen, was wann zu machen war. Im Arbeitsauftrag steht, dass die Schüler es im Heft aufschreiben und sich notieren sollen, was man da macht. Das hätte Sohnemann sicher nicht machen wollen.
Die Herleitung der pq-Formel hat er ansatzweise hinbekommen. Hier wäre sich die Zusammenarbeit mehrerer guter Schüler sinnvoll, die gemeinsam daran arbeiten. Die „schnelle“ Truppe könnte dann die Herleitung der pq-Formel der restlichen Klasse vorstellen, die vielleicht etwas langsamer ist. Oder sie unterstützen die langsameren Schüler, dass die selber die Formel herleiten können.
Fazit
Mit meiner „privaten“ Testperson hat es eigentlich so funktioniert wie es wollte. Ich musste ihn allerdings mit einer Belohnung für morgen etwas motivieren. Da er eher etwas besser in Mathe ist, stellt er sicher nicht den Durchschnitt einer Mathe-Klasse dar. Daher würde ich mich über eure Erfahrungen auch auch weitere Ideen freuen.
Antworten