Nach den grundlegenden Umformungen kommen wir zum Distributiv-Gesetz, dann die Arbeit. Viele Schülern fällt es schwer. Ich habe in H5P ein paar Übungen im Vorraus rausgeworfen, wo es um Flächen von Rechtecken bzw. aufgeteilten Rechtecken ging. Da gab es viele Fehler … daher einige Übungen zum Distributiv-Gesetz in verschiedenen Tools. Ihr dirft daran teilhaben …
(1) GraspableMath – einfaches Einsetzen
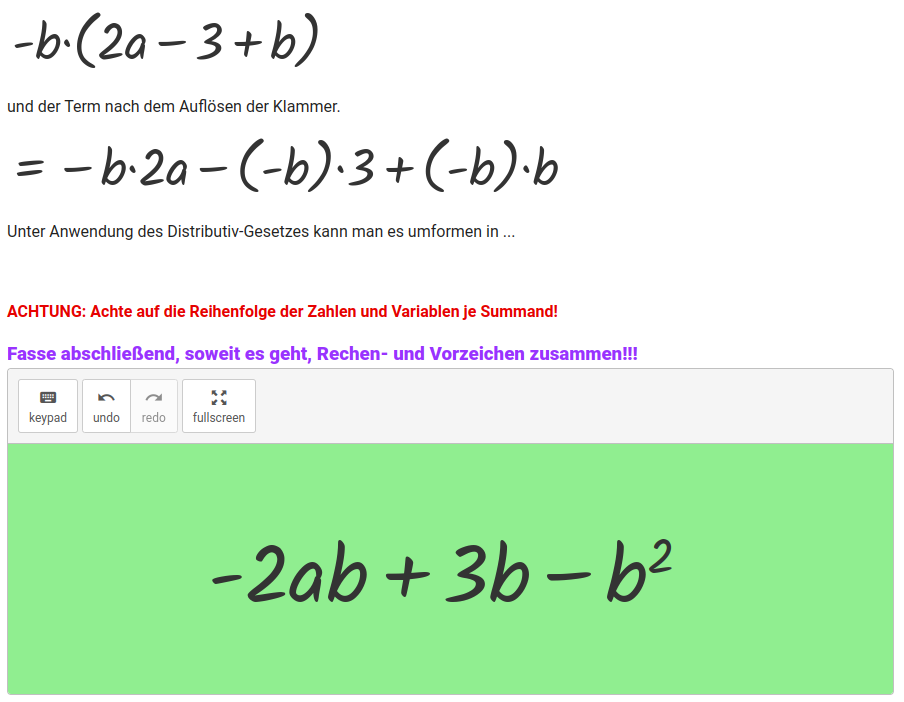
Im Prinzip ist das mit dem Distributiv-Gesetz ein recht einfaches Schema. Denoch fällt es einigen Schülern schwer. Dank eines Kollegen aus Amerika, der auch in GeoGebra aktiv und bekannt ist, hatte ich eine Idee, wie in den GraspableMath das Einsetzen/Eingeben von Wert ermöglichen kann. Es gibt nämlich einen Platzhalter und GraspableMath schaut, ob die Eingabe richtig ist. Dies ist wenig empfindlich als eine Eingabe in einem Lückentext und dank der eingeblendeten Tastatur, kann es keine Fehler wegen einem falschen Symbol geben.
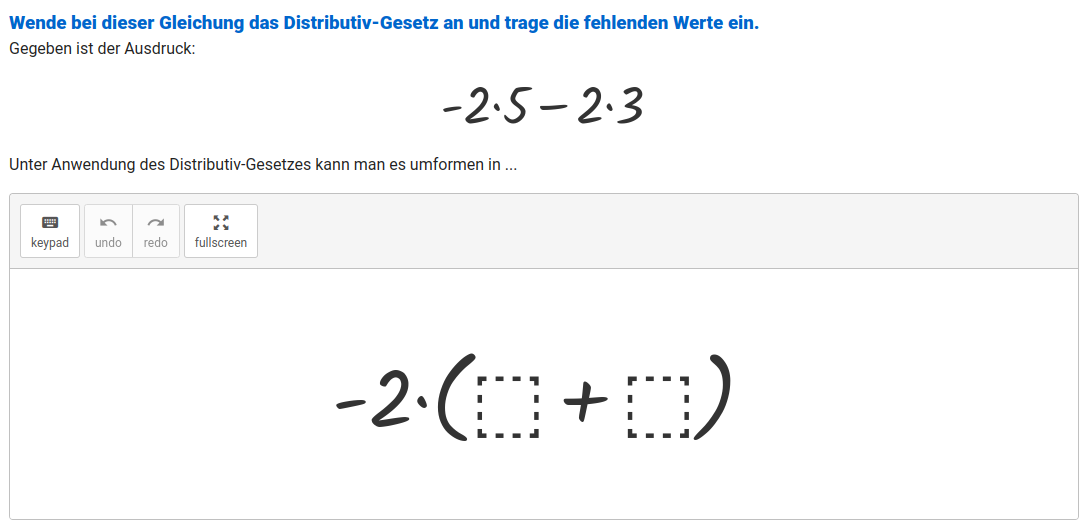
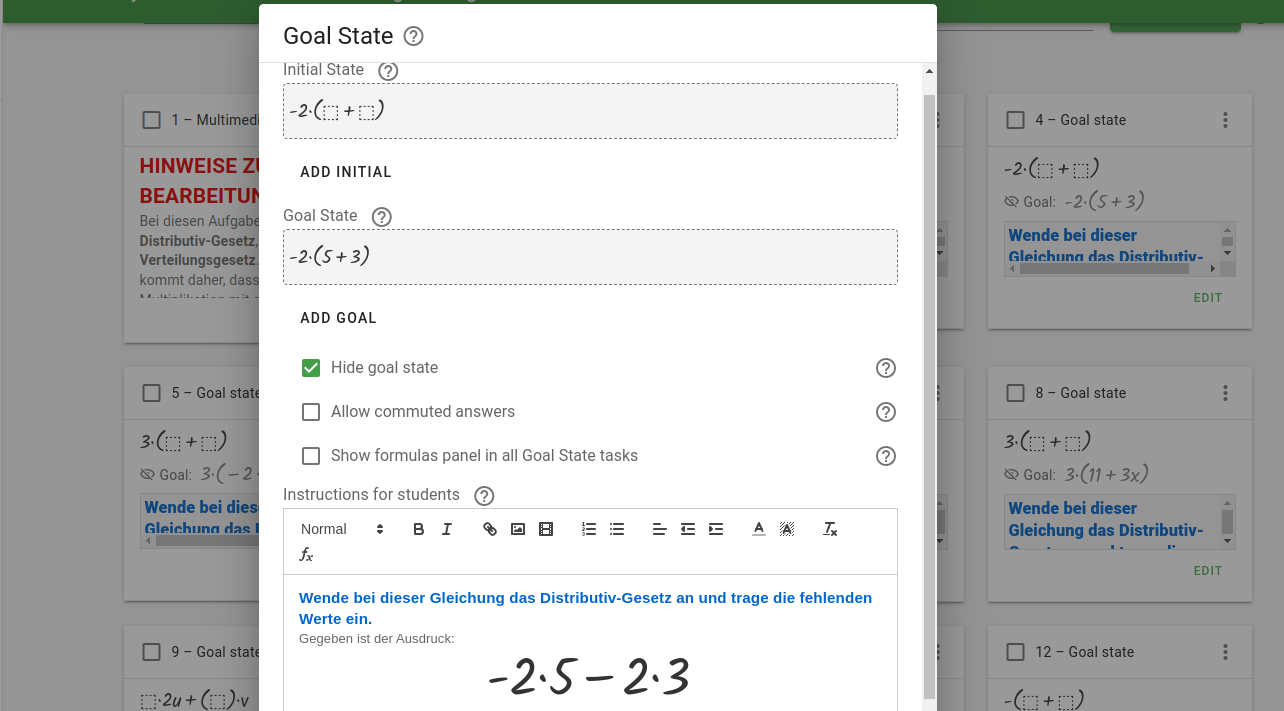
Dieses einfache Einsetzen wird mit der Zeit etwas zu langweilig. Eventuell könnte man diese Übung besseren Schülern erlassen und ergänzend etwas schweres anbieten.
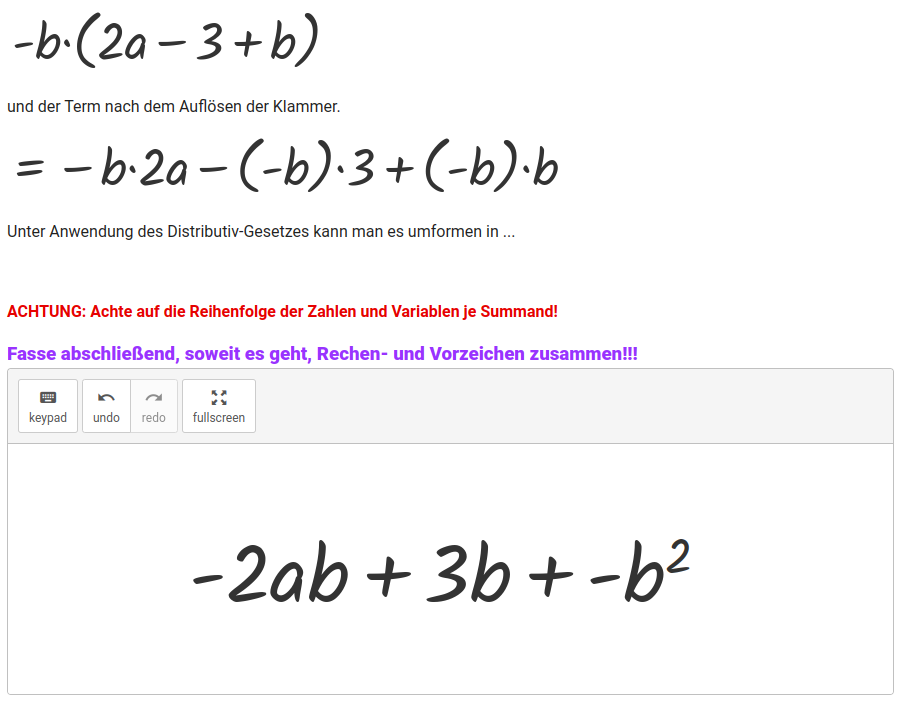
Ich habe aber versucht verschiedene Schwierigkeiten unterzubringen, auch das Ausklammern, wo teilweise etwas gegeben ist.
Und am Ende muss etwas nicht nur eingeben sondern dann noch vereinfacht werden. Da ist das Problem, dass ich zwischen den Eingabe-Feldern immer ein Rechenzeichen haben muss. Lasse ich ein „Plus“ weg, dann interpretiert GraspableMath das als „Mal“. Ich habe überlegt, ob das schlimm ist, aber im Prinzip denkt man am besten eh im Sinne von „lauter Summanden“.
Hier das Material:
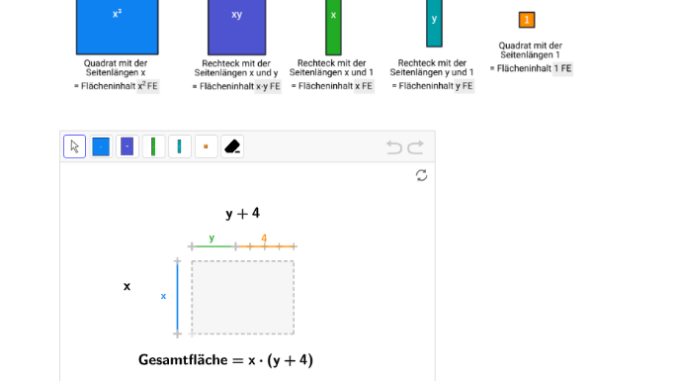
Distributiv-Gesetz als Fläche von zerlegten Rechtecken interpretieren
Das mache ich schon seit einiger Zeit so und habe auch ein Arbeitsblatt dazu, wo die Schüler Zeichnungen vorgeben haben, die sie ergänzen und beschriften müssen. Die Lösung gibt es in moodle.
Wie schon erwähnt ist das auch für die Schüler nicht so einfach. Seit einiger Zeit gibt es in Mathigon die sogenannten Algebra-Tiles. Man kann hier das Distributiv-Gesetz verdeutlichen. Soweit ganz nett und gerade wenn man mal auf die Schnelle etwas verdeutlichen will, dann kann ich schnell in GraspableMath das aufrufen. Die Idee war, den Schülern dort auch Aufgaben zu geben, aber … es ist keine Kontrolle möglich. Bei einer Tablet-Klasse könnte ich die Schüler beauftragen Screenshots zu sammeln und dann vielleicht abzugeben. Da ich die Tablets aber nur zeitweise nutze passte das nicht.
Dann bin ich auf die Idee gekommen, das in GeoGebra zu machen und die Veröffentlichung als „Einheit“ zu nutzen, um zu sehen, ob die Schüler das richtige Ergebnis haben. Es gab bereits eine fertige Zeichnung, aber die hat mir nicht so gefallen und so habe ich mal „auf die Schnelle“ eine eigene Zeichnung erstellt und gleich mit ein paar Hilfsmittelchen versehen, etwa das die Längen der Seiten angezeigt werden können. Aus dieser Zeichnungen habe dann extra Zeichnungen als Aufgaben erstellt.
Herausgekommen ist dann ein Buch, das ich als „Einheit“ veröffentliche.

Über die Werkzeuge fügen die Schüler die Teilflächen in die Zeichnung ein, drehen sie bei Bedarf passend und sollen am Ende noch die Summe der Teilflächen angeben. Es gibt zwar keine automatisierte Kontrolle, aber ich sehe, ob die Schüler es richtig haben oder nicht.
Ich finde das passend zu der verherigen Aufgabe in GraspableMath. Im Grund genommen machen Sie fast das gleiche, nur wird es visualisiert und sie können die Lösung eigentlich ablesen. Ziel ist natürlich, dass sie das alles zusammen bekommen.
Fazit nach einer Anwendung
So richtig zufrieden bin ich nicht. Zum einen habe ich noch Ideen für eine Verbesserung der Zeichnung in GeoGebra. Zum anderen muss ich noch mal umdenken, was die grundsätzliche Idee betrifft. Die Grundlage für diese Anwendung ist die Idee einer Art Vierfelder-Tafel, wobei die Flächen für die vier Produkte stehen, die man bei einer Multiplikation wie (a + b)(c + d) herauskommen.
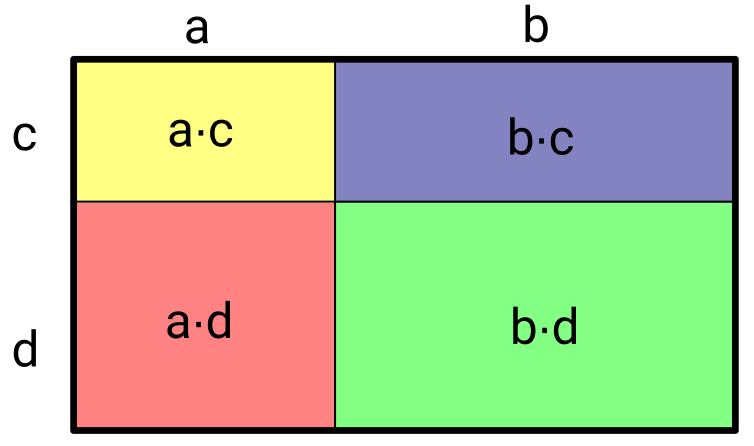
Da denke ich, muss man mehr Wert darauf legen, bei Zahlen diese nicht getrennt zu betrachten, also etwa bei (x + 5)(x+2) nicht die 5 als 1+1+1+1+1 zu verstehen. Mal schauen …
Antworten